浅谈树和二叉树(二)

Posted on | In | Visitors:

线索二叉树

概述

遍历二叉树是以一定的规则将二叉树中的结点排列成一个线性序列，得到二叉树中结点的先序序列，中序序列和后序序列。这实质上是对一个非线性序列进行线性化操作，使得每个结点（除第一个和最后一个）都有唯一的前驱和后继。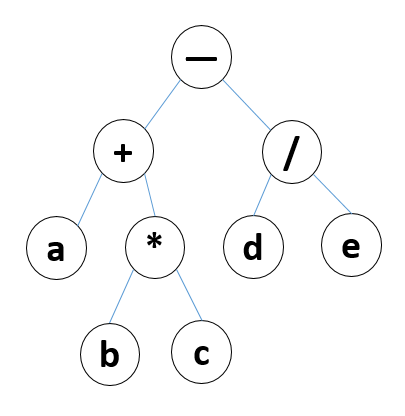


在该图中的中序遍历结果为：a+b*c-d/e。’c’的前驱是’*‘，后继是’-‘

对于二叉树的存储结构在上一篇文章已经说过了，回忆下二叉链表的结构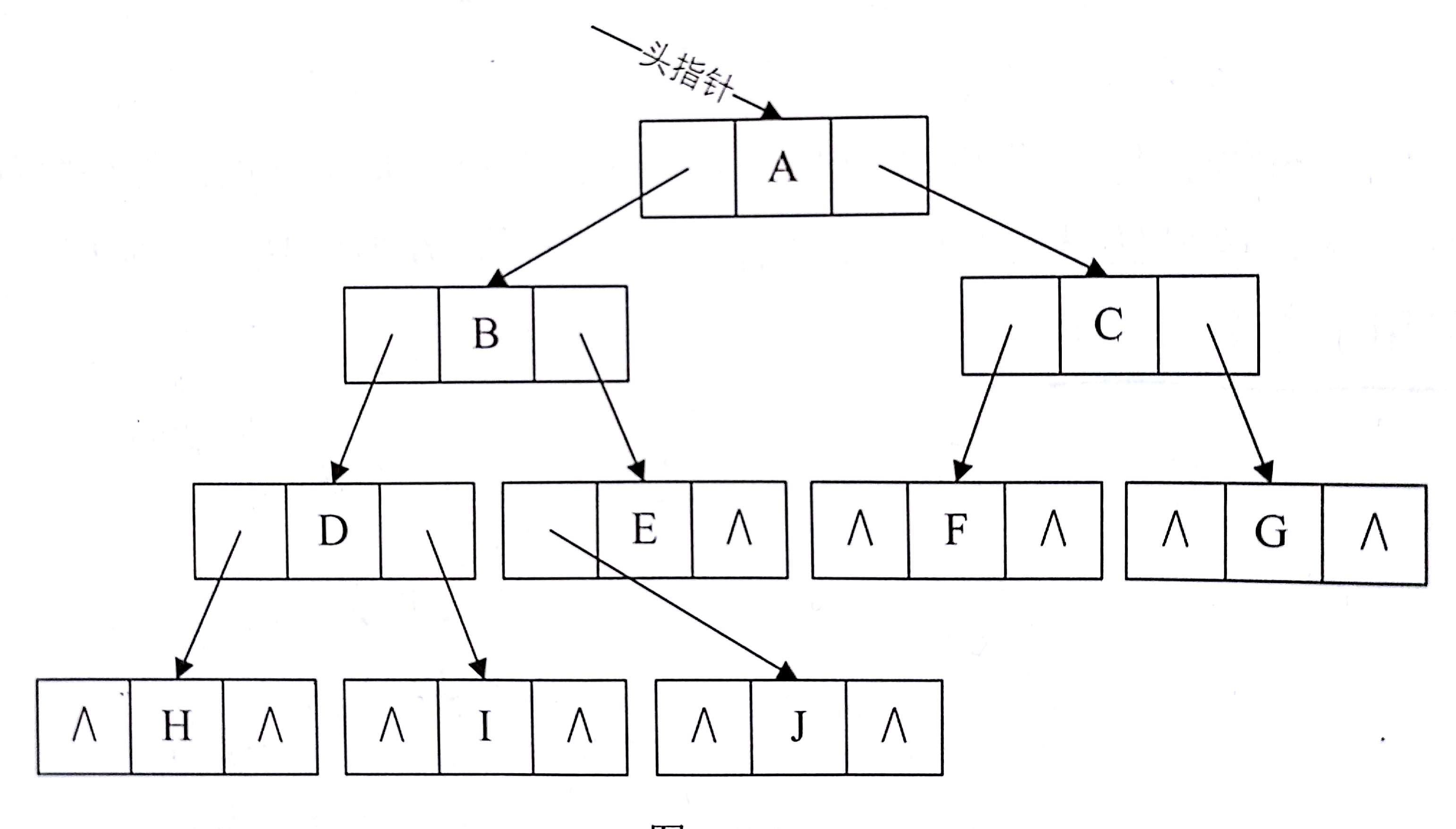
可以发现其中有好多指针域都是空（“^”）着的。若有n个元素，则共有2n个指针域，n-1个分支，也就是说浪费了2n-(n-1)=n+1个指针域的资源。
在二叉链表中，我们可以知道每个结点的左右孩子的地址，但是却不知道其前驱是谁，后继是谁，要想知道必须遍历一次。我们完全可以把空闲的指针域用来存储这些前驱与后继的信息。
这种指向前驱和后继的指针称为线索，加上线索的二叉链表称为线索链表，相应的二叉树就称为线索二叉树
做如下规定：若结点有左子树，则其lchild指示其左孩子，否则指示其前驱；若结点有右子树，则其rchild指示其右孩子，否则指示其后继，为避免混淆，可以增加两个标志位LTag和RTag：

于是乎，将上图的二叉树线索化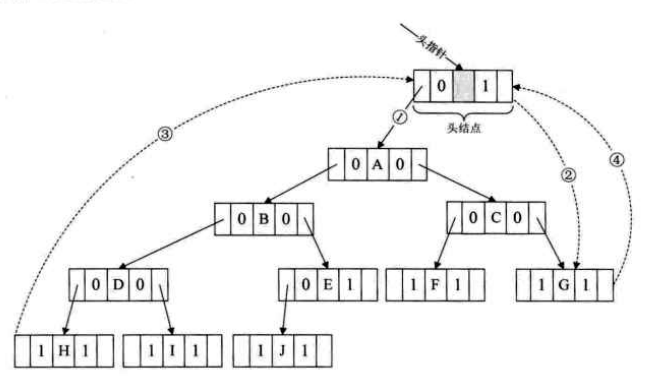

实现

1
2
3
4
5
6
7
8
9
10
//存储结构如下
typedef enum{Link,Thread} PointerTag;
//Link=0表示指向左右孩子的指针，Thread=1表示指向前驱或后继
//二叉线索存储结点结构
typedef struct BiThrNode{
    TypeName data;
    struct BiThrNode *lchild,*rchild;
    PointerTag LTag;
    PointerTag RTag;    //左右标志
}

为了记录下访问结点的先后关系，设定一个pre指针指向刚刚访问过的结点。
中序遍历算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//递归版
BiThrTree pre = NULL;
void InThreading(BiThrTree *p){
    InThreading(p->lchild);    //递归左子树线索化
    if(!p->lchild){    //没有左孩子
        p->LTag = Thread;    //前驱线索
        p->lchild = pre;    //左孩子指针指向前驱
    }
    if(!pre->rchild){    //前驱没有右孩子
        pre->RTag = Thread;    //后继线索
        pre->rchild = p;    //前驱右孩子指向后继p
    }
    pre = p;
    InThreading(p->rchild);    //递归右子树线索化
}

很容易发现，和二叉树的中序遍历代码结构完全一样，只是将打印结点改成线索化功能。
上图中设置一个头结点，令其lchild指向二叉树的根结点，rchild指向中序遍历的最后一个结点，反之，将中序遍历的第一个结点的lchild指向头结点，最后一个结点的rchild指向头结点，如此定义后，我们既可以从第一个结点起顺后继进行遍历，也可以从最后一个结点起顺前驱进行遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//迭代版
void Travser(BiTree *T){    //T 为二叉树的头结点
    BiTree *p = T->lchild;    //p指向根结点
    while(p != T){
        while(p->LTag == Link)    //有左子树
            p = p->lchild;    //该循环结束时p指向第一个结点
        printf("%c",p->data);
        while(p->RTag == Thread && p->rchild != T){
            p = p->rchild;
            printf("%c",p->data);    //打印其后继结点
        }
         p = p->rchild;    //p进入其右子树
    }
}

对上图的运行打印结果应为：HDIBJEAFCG
从代码可以看出，其实就是一个链表的遍历，时间复杂度O(n)，又充分利用了空指针域，节省了空间。所以，如果所采用的二叉树需要经常遍历或查找结点时需要某种遍历的前驱或后继，用线索二叉链表的存储结构是非常不错的选择

树，森林，二叉树的转换

树转换为二叉树

  1. 加线。在所有兄弟结点之间加一条连线。
  2. 去线。对树中的每个结点，只保留它与第一个孩子结点的连线，删除它与其他孩子结点之间的连线。
  3. 层次调整。以树的根为轴心，将整棵树旋转一定角度使之结构层次分明。注意第一个孩子是二叉树结点的左孩子，兄弟转换过来的孩子是结点的右孩子

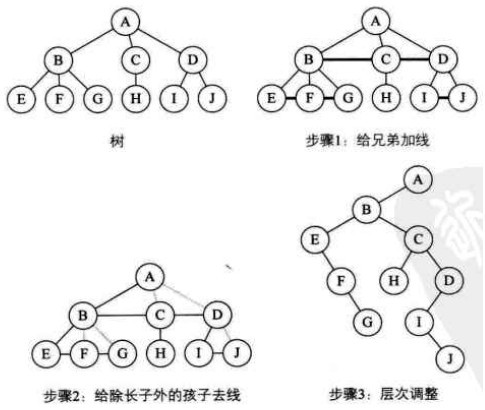
森林转换为二叉树

森林是由若干棵树构成的，所以可以理解为森林中的每棵树都是兄弟，可以按照兄弟的处理来进行

  1. 将每棵树转换为二叉树
  2. 从第二棵树开始，将每棵树的根结点作为前一棵树的右孩子，用线连接。

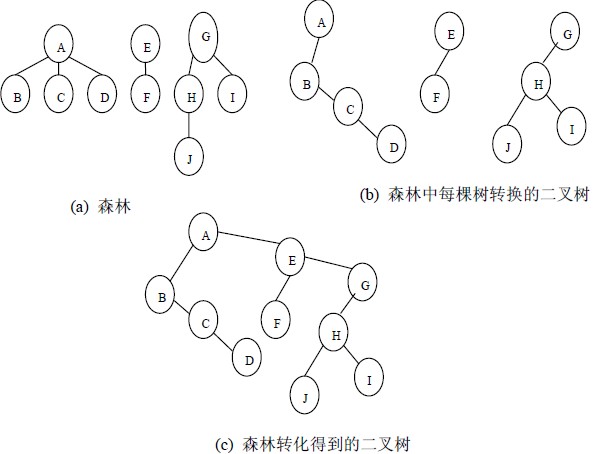
二叉树转换为树

其实就是树转二叉树的逆过程

  1. 加线。如果结点存在左孩子，则将其左孩子的右孩子，左孩子的右孩子的右孩子…反正就是它的左孩子的所有右孩子都与该结点连接。
  2. 去线。将原二叉树中的所有与右孩子相连接的线都去掉。
  3. 层次调整。使树层次结构分明

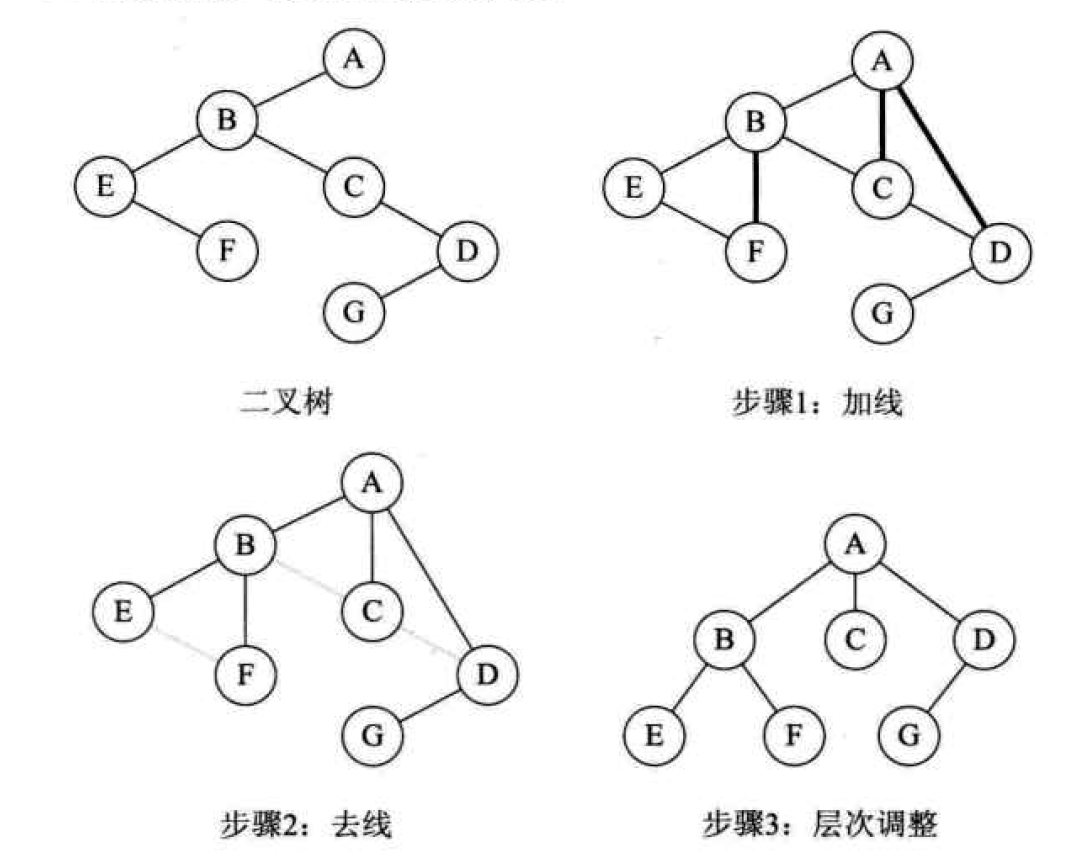
二叉树转换为森林

森林转换为二叉树是将第二棵开始的所有的树都连到前一个的右子树上， 所以判断一棵二叉树能转换为一棵树还是森林的标准就是看它的根结点有没有右子树，有则表示能转换为森林，否则就只能转换为一棵树。转换步骤如下

  1. 将二叉树的根结点与其右子树断开，看断开后的二叉树，如果还有右子树，继续断开。
  2. 将各二叉树转换为树

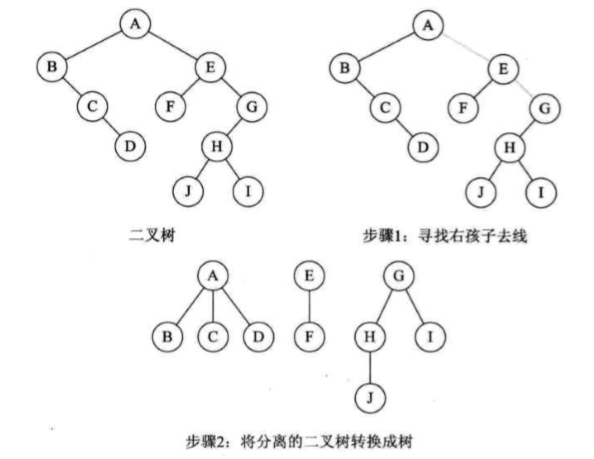
    简单分析可以发现，二叉树的先序遍历和森林的先序遍历相同；二叉树的中序遍历和森林的后序遍历相同。这也就是说，当以二叉链表作树的存储结构时，树的先根遍历和后根遍历可以借用二叉树的先序遍历和中序遍历来实现。

最优二叉树

概述

从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径，路径上的分支数目称做路径长度，树的路径长度是从根结点到每个结点的路径长度之和（完全二叉树即树路径长度最短的二叉树）。
考虑一般情况，即带权的结点，结点的带权路径长度是根结点到该结点的路径长度与该节点的权值得乘积。树的带权路径长度为树中所有叶子结点的带权路径长度的和，记作WPL。
假设有n个权值，构造一棵有n个叶子结点的二叉树，其中带权路径长度最小的二叉树称为最优二叉树或赫夫曼树

算法描述

  1. 根据给定的n个权值{W1,W2,…Wn}构成n棵二叉树集合F= {F1,F2,…Fn}，每棵二叉树Fi只有一个带权根结点Wi，左右子树均为空。
  2. 从F中选取两棵根结点的权值最小的树作为左右子树构成一棵新的二叉树，新二叉树的根结点权值为左右子树的权值得和。
  3. 从F中删除这两棵树，同时将新构成的二叉树加入其中。
  4. 重复（2）和（3），直到F只有一棵树为止。这棵树便是赫夫曼树

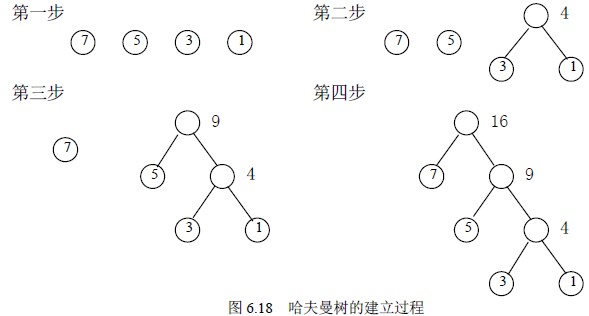
赫夫曼编码

在报文传送过程中，需要将文字转换为二进制字符串，每个字符用一组二进制编码表示。传送过程中肯定希望总长尽可能的短，若要设计长短不一的编码，则必须任意字符的编码都不是另一个字符编码的前缀，这就是前缀编码。
一般的，设需要编码的字符集为d = {d1,d2,…dn}，各个字符在电文中出现的次数或频率为w = {w1,w2,…wn}，以d集合作为叶子结点，w集合作为相应的叶子结点的权值来构造一棵赫夫曼树。规定赫夫曼树的左分支代表0，右分支代表1，则从根结点到叶子结点所经过的路径分支组成的0和1的序列便为该结点对应字符的编码，这就是赫夫曼编码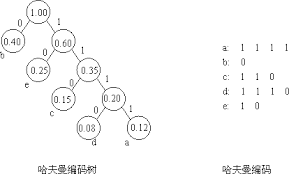

参考书籍：
《数据结构——严蔚敏》
《大话数据结构——程杰》
《数据结构——从概念到C实现》