树
基本术语
- 结点拥有的子树称为结点的度
- 度为0的结点称为叶子结点或终端结点
- 树的度是树内各结点的度的最大值
- 结点的层次从根开始定义,根为第一层,根的孩子为第二层,若某结点的层次为m,则其子树的根就在第m+1层。
- 树中结点的最大层次称为树的深度或高度
- 一棵深度为k且有2^k-1个结点的二叉树称为满二叉树,其每一层上的结点数都是最大结点数
- 从根节点开始,从上到下,从左到右依次填充的二叉树称为完全二叉树,其叶子节点只可能出现在层次最大的两层上面
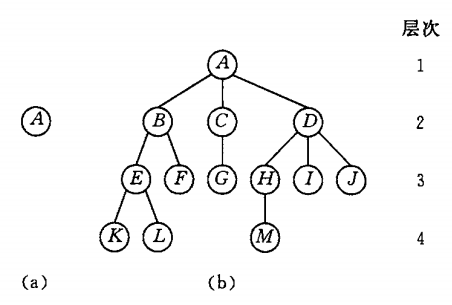
二叉树
定义
每个结点至多只有两棵子树(即二叉树不存在度大于2的结点),并且二叉树的子树有左右之分,次序不能颠倒
性质
在二叉树的第i层上至多有2^(i-1)个结点
1
2
3
4
5
6证明:
当i=1时,2^(1-1)=1;命题成立。
假设j = i-1时命题成立,即第i-1层有2^(i-2)个结点。
当j = i时,由于二叉树的每个结点的度至多为2,
故第i层是第i-1层的2倍,即第i层有2*2^(i-2) = 2^(i-1)个结点。
证毕深度为k的二叉树最多有2^k-1个结点
1
2
3
4
5证明:
第i层至多有2^(i-1)个结点。由等比数列求和公式得
S = a1(1-q^n)/(1-q) = (a1-an*q)/(1-q)
= 2^0(1-2^k)/(1-2)
= 2^k-1对于一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0 = n2+1
1
2
3
4
5
6
7
8
9
10证明:
设度为1的结点个数为n1,总的结点个数为n,则
n = n0+n1+n2 //①
设树的分支数为B,除了根节点外,每个结点都有一个分支进入,则
n= B+1 //②
又所有的分支均为度是2或1的结点产生,则
B = n1+2*n2 //③
由①②③得:
n0 = n2 + 1
证毕具有n个结点的完全二叉树的深度为ceil(log(n+1))
注:logn即以2为底数,ceil(x)即不小于x的最大整数1
2
3
4
5
6
7
8
9
10证明:
假设深度为k,则n满足:
2^(k-1)-1<n<=2^k-1
即
2^(k-1)<n+1<=2^k
两边求对数得:
k-1<log(n+1)<=k
又k是整数,故
k = ceil(log(n+1))
证毕对一棵含有n个结点的完全二叉树按层序编号,从上到下,从左到右,对于任意结点i:
(i>=1),其左孩子编号为2i,如果2i>n,则其没有左孩子;右孩子编号为2i+1,如果2i+1>n,则没有右孩子;i的双亲为floor(i/2);结点i所在的层次为floor(logi)+1。
(i>=0),其左孩子编号为2i+1,如果2i+1>n,则其没有左孩子;右孩子编号为2i+2,如果2i+2>n,则其没有右孩子;i的双亲为floor((i-1)/2),结点0没有双亲;结点i所在的层次为floor(log(i+1))+1。
存储结构
顺序存储
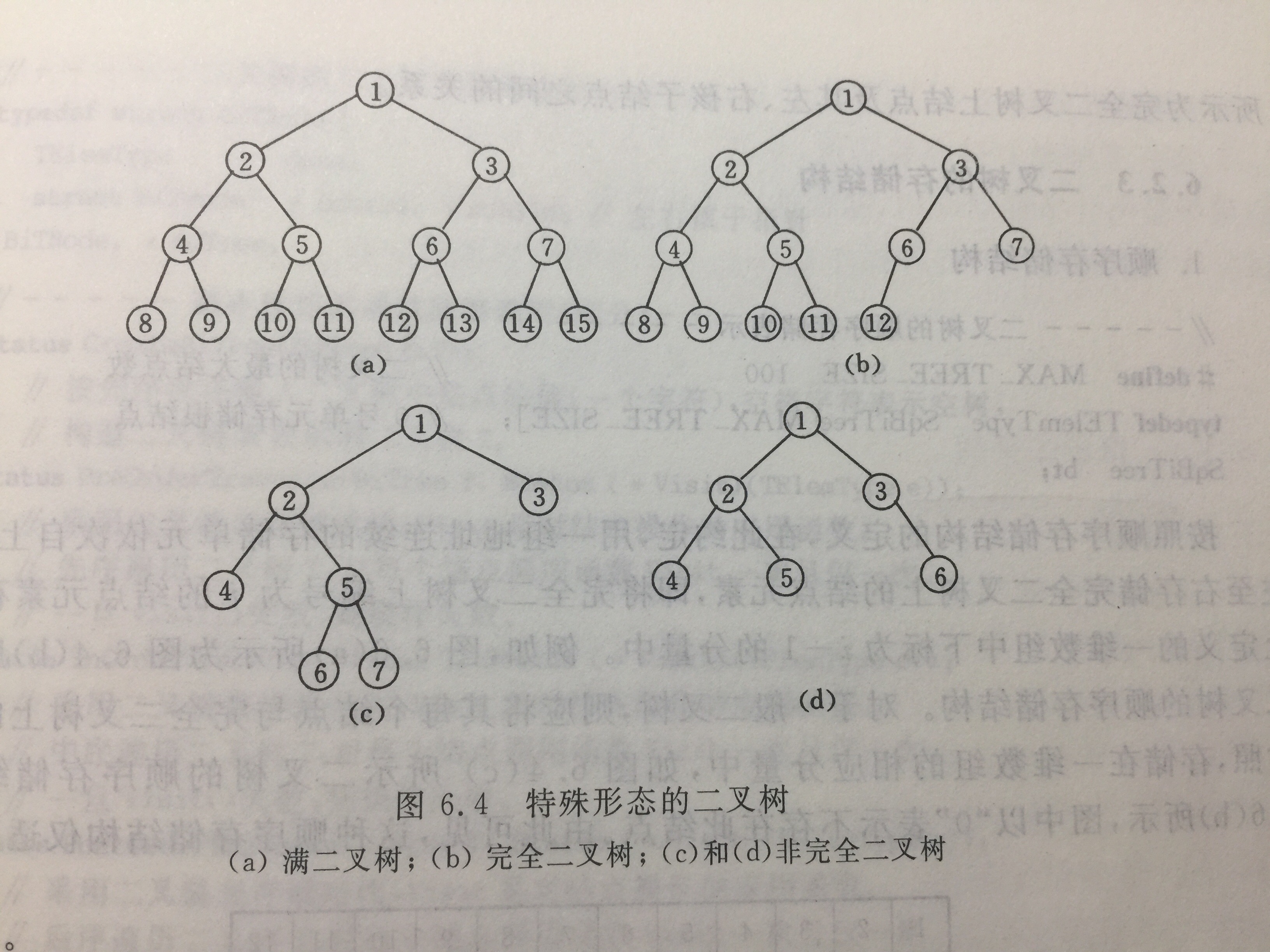
用一组地址连续的存储单元依次自上而下,从左到右存储完全二叉树上的结点元素,即将完全二叉树的编号为i的元素存储到定义的一维数组下标为i-1的位置。
对图6.4的b和c的顺序存储情况如下:
以“0”表示不存在该结点。可见,这种顺序存储只适用于完全二叉树,在最坏的情况下,存储一个深度为k的单支非完全二叉树需要2^k-1的空间的一维数组(实际上只有k个元素)。
链式存储
由二叉树的定义可知,二叉树的节点由一个数据元素和分别指向其左右子树的两个分支构成,则表示二叉树的链表中至少包含三个域:数据域,左右指针域,有时为了便于找到结点的双亲,还可以加一个指向双亲的指针域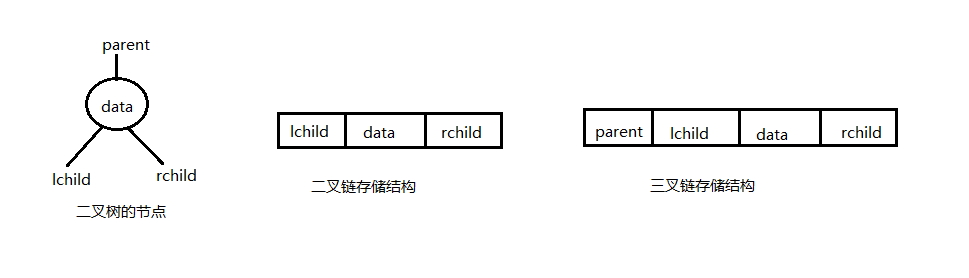
利用这两种结点结构所得的二叉树的存储结构分别称为二叉链表和三叉链表,链表的头指针指向二叉树的根结点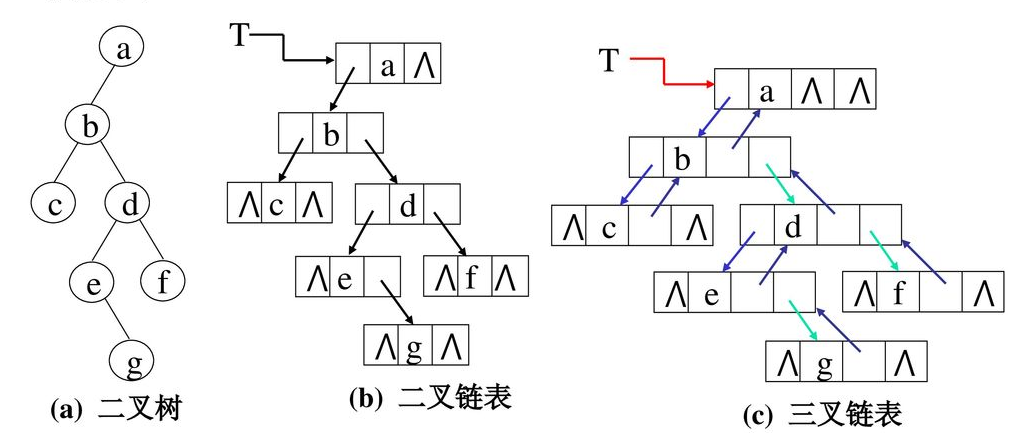
1
2
3
4
5
6typedef struct BiTree{
char data;
struct BiTree *lchild;
struct BiTree *rchild;
//struct BiTree *parent;
};
二叉树的遍历
二叉树的遍历是指从根节点出发,按照某种次序依次访问二叉树中所有的结点,使得每个结点都被访问一次且仅被访问一次
前序遍历
规则:如果二叉树为空,则返回,否则先访问根节点,然后前序遍历左子树,再前序遍历右子树1
2
3
4
5
6
7void preOrder(BiTree *root){
if(root == NULL)
return ;
print(root->data);
preOrder(root->lchild);
preOrder(root->rchild);
}
中序遍历
规则:如果二叉树为空,则返回,否则先中序遍历左子树,然后访问根结点,再中序遍历右子树。1
2
3
4
5
6
7void InOrder(BiTree *root){
if(root == NULL)
return ;
InOrder(root->lchild);
print(root->data);
InOrder(root->rchild);
}
后序遍历
规则:如果二叉树为空,则返回,否则先后序遍历左子树,然后后序遍历右子树,再访问根结点,即从左到右先叶子后结点的方式遍历访问左右子树,最后访问根结点。1
2
3
4
5
6
7void PostOrder(BiTree *root){
if(root == NULL)
return ;
PostOrder(root->lchild);
PostOrder(root->rchild);
print(root->data);
}
层序遍历
规则:如果二叉树为空,则返回,否则从根结点开始,从上到下逐层遍历,同一层中按从左到右的顺序对结点逐个访问。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17//先访问的结点其左右孩子也要访问,符合队列的操作特性,故用一个队列存放已访问的结点
void levelOrder(BiTree *root){
if(root == NULL)
return ;
BiTree *bt = NULL;
queue<BiTree> q;
q.push(root);
while(!q.empty()){
bt = q.front();
q.pop();
print(bt->data);
if(bt->lchild != NULL)
q.push(bt->lchild);
if(bt->rchild != NULL)
q.push(bt->rchild);
}
}
二叉树的建立与销毁
建立
二叉树的建立方法有很多种,一种简单又常见的方法是 根据一个结点序列来建立二叉树。由于前序,中序,后序序列中的任何一个都不能唯一的确定一个二叉树,所以不能直接使用。
建立方法如下:将二叉树中每个结点的空指针引出一个虚结点,其值为一个特定的值,如“#”,以标识其为空,这样处理后的二叉树称为原二叉树的扩展二叉树,扩展二叉树的一个遍历序列就能唯一确定一棵二叉树。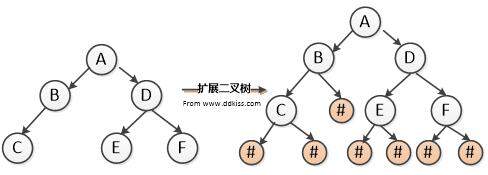
如该图的扩展二叉树的前序遍历为:ABC###DE##F##1
2
3
4
5
6
7
8
9
10
11
12
13BiTree * createBiTree(BiTree *root){
char ch;
scanf("%c",&ch);
if(ch == '#')
root = NULL; //递归结束,建立一棵空树
else{
root = (BiTree *)malloc(sizeof(BiTree));
root->data = ch;
root->lchild = createBiTree(root->lchild);
root->rchild = createBiTree(root->rchild);
}
return root
}
销毁
二叉链表是动态存储分配,其结点是在程序运行时动态申请的,故在二叉链表变量退出其作用域时要释放二叉链表的存储空间。可以对二叉链表进行后序遍历,在访问结点时进行释放处理。1
2
3
4
5
6
7void destroy(BiTree *root){
if(root == NULL)
return;
destroy(root->lchild);
destroy(root->rchild);
free(root);
}
参考资料:
《数据结构——严蔚敏》
《数据结构——殷人昆》
《大话数据结构——程杰》