红黑树详解

Posted on | In | Visitors:


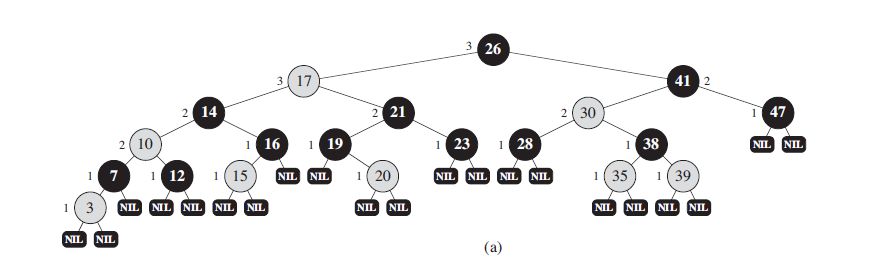
性质

1·所有节点的颜色只可以为红色或者黑色
2·根节点为黑色
3·叶子节点(NIL)为黑色
4·一个红色节点的子节点为黑色
5·任意一个节点到该节点的后代叶子节点的简单路径上所经历的黑色节点数目相同

可以用一个哨兵节点T.NIL来代替所有的叶子节点的NIL孩子和根节点的父节点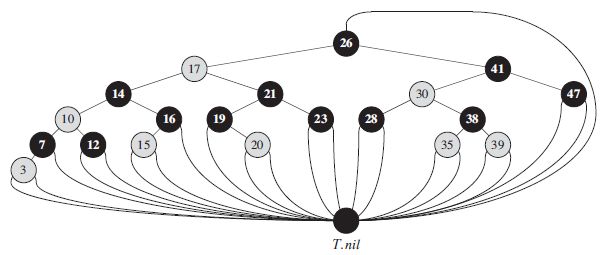

结论

设h是红黑树的高度（不包括外结点），n是树中内结点的个数，r是根结点的黑高度。则：

  1. h<=2r。即红黑树的高度不超过黑高度的2倍
  2. n>=2^r-1。即红黑树的内结点的总数至少为2^r-1
  3. h<=2log(n+1)。即，含有n个内部节点红黑树的高度至多为2log(n+1).由1,2得
    证明：
1
1. 由性质4可知，如果h>2r，则意味着有两个红色的节点相邻。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
3. 先证明：以x为根的子树内含有2^(bh(x))-1个结点。bh(x)为x的黑高。
用数学归纳法：
当x为根时，bh(x) = 0；
2^0-1 = 0;即根的内部节点数为0.

当x不为根时，它的两个子节点的黑高为bh(x)-1 (黑) 或bh(x) (红);
因为x的子节点比x要低，所以假设x的子节点所在子树的内部节点至少有
2^(bh(x)-1)-1个.

故x为根的子树内部节点总数至少为：
2^(bh(x)-1)-1 + 2^(bh(x)-1)-1 + 1
= 2^(bh(x))-1

故结论成立。
设红黑树的高度为h，可得根结点的黑高至少为h/2.
即：n>=2^(h/2)-1.
移项，取对数后得：
h<=2log(n+1)

由结论3可以得出，在红黑树上的操作可以在O(logn)时间内完成。

操作

左旋

节点x的右子节点z不为NIL，左旋即以xz的连接为轴逆时针旋转，使得z为x的父节点，x为z的左子节点，z原来的左子节点连接到x的右子节点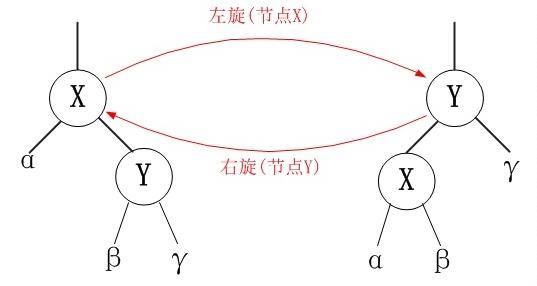

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
左旋
LEFT-ROTATE(T, x){  
    y = x.right             // 假设x的右孩子为y
    x.right = y.left        // 将 “y的左孩子” 设为 “x的右孩子”
    y.left.parent = x       // 将 “x” 设为 “y的左孩子的父亲”
    y.parent = x.parent     // 将 “x的父亲” 设为 “y的父亲”
    if x.parent == T.NIL       
         then T.root = y           // 情况1：如果 “x的父亲” 是空节点，则将y设为根节点
    else if x == x.parent.left  
         then x.parent.left = y    // 情况2：如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
         else x.parent.right = y   // 情况3：(x是它父节点的右孩子) 将y设为“x的父节点的右孩子”
    y.left = x                     // 将 “x” 设为 “y的左孩子”
    x.parent = y                   // 将 “x的父节点” 设为 “y”
}
时间复杂度：O（1）

对x左旋即将它的右孩子节点旋转为它的父亲节点

右旋

1
2
3
4
5
6
7
8
9
10
11
12
13
14
RIGHT-ROTATE(T, y){  
    x = y.left              // 假设y的左孩子为x。下面开始正式操作
    y.left = x.right        // 将 “x的右孩子” 设为 “y的左孩子”，即 将β设为y的左孩子
    x.right.parent = y      // 将 “y” 设为 “x的右孩子的父亲”，即 将β的父亲设为y
    x.parent = y.parent     // 将 “y的父亲” 设为 “x的父亲”
    if y.parent == T.NIL       
        then T.root = x     // 情况1：如果 “y的父亲” 是空节点，则将x设为根节点
    else if y = y.parent.right  
        then y.parent.right = x   // 情况2：如果 y是它父节点的右孩子，则将x设为“y的父节点的左孩子”
    else y.parent.left = x         // 情况3：(y是它父节点的左孩子) 将x设为“y的父节点的左孩子”
    x.right = y                    // 将 “y” 设为 “x的右孩子”
    y.parent = x                   // 将 “y的父节点” 设为 “x”
}
时间复杂度：O（1）

对x右旋即将它的左孩子节点旋转为它的父亲节点

插入

插入节点z，将其染为红色，时间复杂度：O（lgn）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
RB-INSERT(T, z){  
    y = T.NIL                        // 新建节点“y”，将y设为空节点。
    x = T.root                       // 设“红黑树T”的根节点为“x”
    while(x != T.NIL){               
        y = x
        if(z.key < x.key)               
            x = x.left               //情况1.z的值小于当前节点x的值，x向左走
        else 
            x = x.right              //情况2.z的值大于当前节点x的值，x向右走
    }
    z.parent = y
    if(y == T.NIL)
        T.root = z                   //树为空时，插入为根节点
    else if(z.key < y.key)
        y.left = z
    else
        y.right = z
    z.color = RED                    // 将z着色为“红色”
    RB-INSERT-FIXUP(T,z)
                        // 通过RB-INSERT-FIXUP对红黑树的节点进行颜色修改以及旋转，让树T仍然是一颗红黑树
}

调整

插入节点z后被破坏的性质有性质2和性质4，如果插入为根节点，则性质2被破坏，如果插入节点的父节点为红色，则性质4被破坏
如果违反性质2，则说明插入的为根节点
处理：将其染成黑色
如果违反性质4，则有三种情况：
case1：z和z.parent都为红色，z的叔叔节点为红色
处理：将z.parent染为黑色，z.parent.parent染为红色，z.uncle染为黑色。

case2：z和z.parent都为红色，z的叔叔为黑色，z == z.parent.right
处理：z = z.parent，以z为支点，左旋

case3：z和z.parent都为红色，z的叔叔为黑色，z == z.parent.left
处理：z.parent染为黑色，z.parent.parent染为红色，以z.parent.parent为支点右旋

参考资料：
《算法导论》