平衡二叉树（AVL树）详解

Posted on | In | Visitors:

概述

平衡二叉树又称为AVL树，它或者是一棵空树，或者是具有以下性质的二叉搜索树：

  1. 根结点的左子树和右子树的深度最多相差1
  2. 根结点的左子树和右子树也都是平衡二叉树

结点的平衡因子是该结点的左子树与右子树深度的差。显然在平衡二叉树中平衡因子的取值只可能为-1,0,1。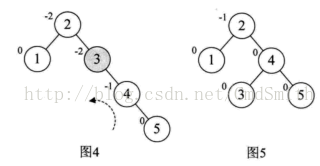
(显然图4不是平衡二叉树)
最小不平衡子树是指在平衡二叉树的构造过程中，以距离插入节点最近的、且平衡因子的绝对值大于1的结点为根的子树。例如在图4中，插入结点5后，最小不平衡子树为以3所在的结点为根的子树。

构造过程

构造平衡二叉树需要根据新插入的结点和最小不平衡子树根结点之间的关系进行相应的调整。设结点A为最小不平衡子树的根结点，对该子树进行平衡调整有以下4种情况：

  • LL型
    图a为插入前的平衡二叉树，结点x插到结点B的左子树上，导致结点A的平衡因子从1变为2。
    新插入的结点是插在结点A的左子树的左孩子上，故称为LL型。需将支撑点A改为B，顺时针旋转，A和BR发生冲突，根据旋转优先，结点A成为B的右孩子，B的右子树BR成为A的左子树。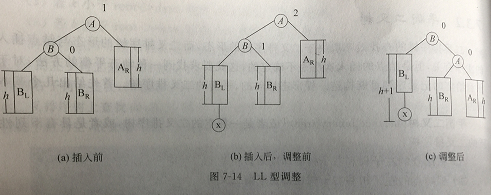
  • RR型
    结点x插入在结点B的右子树上，导致A的平衡因子从-1变为-2。
    新插入的结点是插在结点A的右子树的右孩子上，故称为RR型。需将支撑点由A改为B，逆时针旋转，A与BL发生冲突，结点A成为B的左子树，BL成为A的右子树。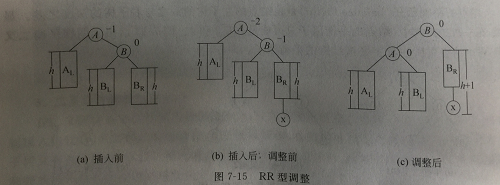
  • LR型
    结点x插入在结点A的左孩子的右子树上，导致A的平衡因子从1变为2。
    这属于LR型，需要进行两次调整。第一次A不动，调整其左子树，将子树支撑点由B改为C，逆时针旋转，B成为C的左子树，CL成为B的右子树。第二次，将支撑点由A改为C，顺时针旋转，A成为C的右子树，CR成为A的左子树。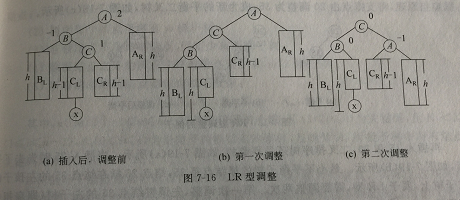
  • RL型
    结点x插入在结点A的右孩子的左子树上，导致A的平衡因子从-1变为-2，这属于RL型，需进行两次调整。第一次A不动，将子树支撑点由B改为C，顺时针旋转，B成为C的右子树，CR成为B的左子树。第二次，将支撑点由A改为C，逆时针旋转，A成为C的左子树，CL成为A的右子树。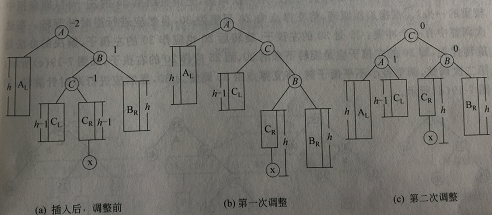

    每插入一个结点，首先从插入结点开始，沿通向根结点的路径开始计算各结点的平衡因子，如果某结点的平衡因子的绝对值超过1，这说明插入操作破坏了平衡二叉树的平衡性，找出最小不平衡子树，根据插入结点与最小不平衡子树根结点的关系判断调整类型，进行相应调整使其再次成为一棵平衡二叉树。

实现

结构相比于二叉搜索树要做出调整：

1
2
3
4
5
typedef struct Binode{
    int data;     //数据成员
    int bf;    //平衡因子
    struct Binode *lchild,*rchild;
}BiNode;

右旋：

1
2
3
4
5
6
void R_route(Binode *root){
    Binode *p = root->lchild;
    root->lchild = p->rchild;
    p->rchild = root;
    *root = p;
}

左旋类似：

1
2
3
4
5
6
void L_route(Binode *root){
    Binode *p = root->rchild;
    root->rchild = p->lchild;
    p->lchild = root;
    *root = p;
}

左平衡旋转处理(LL , LR)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#define LH 1   //左高
#define EH 0   //等高
#define RH -1  //右高
void LeftBalance(Binode *T){
    Binode *L,*Lr;
    L = T->lchild;
    switch(L->bf){
        case LH :    //LL型，新结点插到T的左子树的左孩子结点上，要进行右旋
            L->bf = EH;T->bf = EH;    //看图7-14 B(L)左右都是h+1，A(T)左右都是h
            R_route(T);
            break;
        case RH :    //LR新结点插到T的左子树的右孩子结点上，要进行双旋转
            Lr = L->rchild;
            switch(Lr->bf){
                case LH : 
                    T->bf = RH;L->bf = EH;    //看图7-16 B(L)左h，右h+1，A(T)左h-1,右h
                    break;
                case RH : 
                    T->bf = EH;L->bf = LH;    //脑补类似图7-16 B(L)左h，右h-1，A(T)左右都是h（CR+x）
                    break;
                case EH :    //脑补图7-16，CR=h，CL = h-1，x接到CL上
                    T->bf = L->bf = EH:
                    break;
            }
            Lr->bf = EH;
            L_route(L);    //对T的左子树进行左旋处理
            R_route(T);    //对T进行右旋处理
            break;
    }
}

右平衡旋转处理(RR , RL)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#define LH 1   //左高
#define EH 0   //等高
#define RH -1  //右高
void RightBalance(Binode *T){
    Binode *R,*Rl;
    R = T->rchild;
    switch(R->bf){
        case RH :    //RR型，新结点插到T的右子树的右孩子结点上，要进行左旋
            R->bf = EH;T->bf = EH;    //结合图7-15，调整后A(T)左右都是h，B（R）左右h+1
            L_route(T);
            break;
        case LH :    //RL型，新结点插到T的右子树的左孩子结点上，要进行双旋转
            Rl = R->lchild;
            switch(Rl->bf){
                case LH : 
                    T->bf = EH;R->bf = RH;    //脑补图7-17，x接CL，调整后A（T）左h，右h，B（R）左h-1，右h
                    break;
                case RH : 
                    T->bf = LH;R->bf = EH;    //结合图7-17，调整后A（T）左h，右h-1,B(R)左h，右h
                    break;
                case EH :    //脑补图7-17，CL=h，CR=h-1，x接CR
                    T->bf = L->bf = EH:
                    break;
            }
            Rl->bf = EH;
            R_route(R);    //对T的右子树进行右旋处理
            L_route(T);    //对T进行左旋处理
            break;
    }
}

若在平衡二叉树T中不存在和e有相同关键字的结点，则插入并返回1，否则不插入返回0，若因插入而使树失去平衡，则进行平衡旋转处理，布尔变量taller反映T长高与否。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
bool InsertAVL(Binode *T,int data,bool taller){
    if(!T){
        T = (Binode *)malloc(sizeof(Binode));
        T->data = e;
        T->lchild = T->rchild = NULL;
        T->bf = EH;
        taller = true;
    }
    else{
        if(e == T->data){
            taller = false;
            return false;   //树中以有和e相同的元素
        }
        if(e < T->data){
            if(!InsertAVL(T->lchild,e,taller))
                return false;
            if(taller){
                switch(T->bf){
                    case LH :     //左子树高，又插到左子树，故需左旋调整
                        LeftBalance(T);
                        taller = false;
                        break;
                    case RH :
                        T->bf = EH;
                        taller = false;
                        break;
                    case EH :
                        T->bf = LH;
                        taller = true;
                        break;
                }
            }
        }
        else{
            if(!InsertAVL(T->lchild,e,taller))
                return false;
            if(taller){
               switch(T->bf){
                case LH :
                    T->bf = EH;
                    taller = false;
                    break;
                case EH :
                    T->bf = RH;
                    taller = true;
                    break;
                 case RH :    //右子树高，还插到右子树，故需右旋调整
                    RightBalance(T);
                    T->bf = false;
                    break;
                }
            }
        }
    }
    return true;
}

复杂度分析

在平衡二叉树上进行查找的比较次数最多不超过树的深度。设Nh表示深度为h的平衡二叉树中最少结点个数，则有如下递推关系成立：N0 = 0,N1 = 1,N2 = 2,N3 = 4 … Nh = N(h-1)+N(h-2)+1。（类似斐波那契数列，数学归纳法可证得）。
有n个结点的平衡树的最大深度为logn+1，因此在平衡树上进行查找操作的时间性能为O(logn)

god，终于写完了…
终极目标只有一个，在尽可能早的时候发现不平衡并调整。在左旋平衡（LeftBalance）和右旋平衡（RightBalance）两个函数中，对于各结点的 LH，RH，EH的调整部分可以结合图7-14到7-16中的h变化情况一起看，会比较容易理解。

参考资料：
《数据结构——殷人昆》
《算法导论 3th》
《数据结构——从概念到C实现》
《大话数据结构——程杰》
《数据结构——严蔚敏》