概述
连通图的生成树是包含图中全部顶点的一个极小连同子图。在生成树中添加任意一条属于原图中的边必定会产生回路,因为新添加的边使其依附的两个顶点之间有了第二条路径;在生成树中减少一条边,必然会成为非连同,所以一棵具有n个顶点的生成树有且仅有n-1条边。生成树可能不唯一。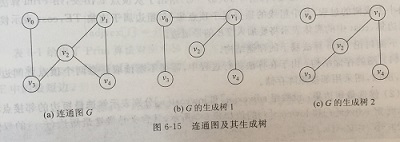
无向连同网的生成树上各边的权值之和称为该生成树的代价,在图的所有生成树中,代价最小的生成树称为最小生成树
Prim算法
基本思想
设G = (V,E)是无向连同网,T = (U,TE)为G的最小生成树。
从初始状态U = {v},T = { }开始,重复:在所有i∈U,j∈V-U的边中找一条代价最小的边(i,j)并入集合TE,同时j并入U。直至U==V。
步骤
输入:一个加权连通图,其中顶点集合为V,边集合为E;
初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {};
重复下列操作,直到Vnew = V:
- 在集合E中选取权值最小的边(u, v),其中u为集合Vnew中的元素,而v则是V中没有加入Vnew的顶点(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);
- 将v加入集合Vnew中,将(u, v)加入集合Enew中;
输出:使用集合Vnew和Enew来描述所得到的最小生成树。
简单的说,就是每次从剩余顶点中选一个离选中的顶点集合距离最短的点。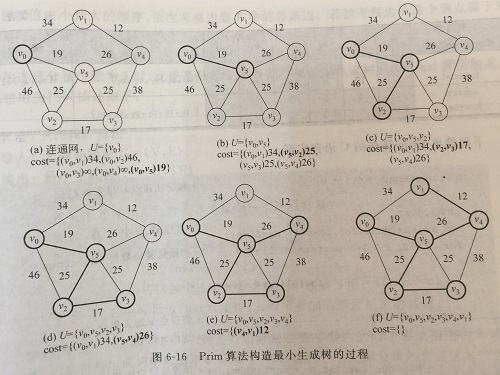
实现
1 | typedef struct{ |
1 | void prim(MGraph *G,int v){ //从顶点v开始 |
复杂度
设n个顶点,初始化要执行n次,第二个for要n-1次,内层for要n次,所以整体复杂度为O(n^2)。与边数无关。适合求稠密网的最小生成树。
Kruskal算法
基本思想
设G = (V,E)是无向连同网,T = (U,TE)为G的最小生成树。
初始状态为U=V,TE = { },T中的各个顶点各自构成一个连同分量,然后按照边的权值从小到大排序,依次考察边集E中的各条边,若其两个顶点属于两个不同的连同分量,则将此边加入到TE中,同时把两个连同分量连接为一个连同分量;若两个顶点属于同一个连同分量,则舍去此边,以免造成回路。如此循环,当T中的连同分量个数为1时完成。
步骤
- 将原图中所有的边按权值从小到大排序
- 从权值最小的边开始,如果这条边连接的两个节点于图G中不在同一个连通分量中,则添加这条边到图G中
- 重复2,直至图G中所有的节点都在同一个连通分量中
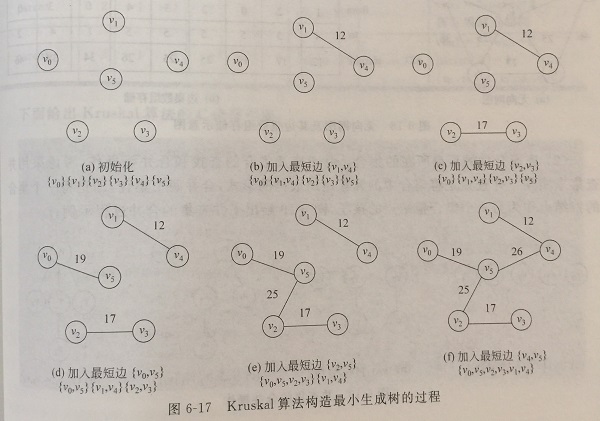
实现
1 | typedef struct { |
1 | bool cmp(EdgeType a,EdgeType b){ |
复杂度
设有n个顶点e条边,初始化要执行n次,第二个for最多e次最少n-1次,Find最少logn次,sort为O(eloge),所以整体时间复杂度为O(eloge),相比较与prim算法,kruskal更适合求稀疏网的最小生成树。
题目集锦
POJ 1251
POJ 1287
HDU 1233
HDU 1875
HDU 5253
HDU 4786
ZOJ 1586
UVA 10766
计蒜客
参考资料:
《数据结构——从概念到C实现》
《大话数据结构——程杰》
《挑战程序设计竞赛》
维基百科 kruskal
维基百科 prim